Pour tout sous-ensemble
Proof.
Soit
 et supposons que
et supposons que
 vect
vect soit dense
dans
soit dense
dans 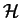 . Alors
. Alors
 . Comme
. Comme
 ,
il existe une suite
,
il existe une suite  d'éléments de
d'éléments de
 convergente vers
convergente vers  .
Or
.
Or
 et
et
 donc
donc  =0. Le
produit scalaire étant continu on a:
=0. Le
produit scalaire étant continu on a:
![$\displaystyle <x_n,x>\xrightarrow[n\longrightarrow \infty]{}<x,x>$](img577.png) Par suite
Par suite
 donc
donc  .
.  étant quelconque dans
étant quelconque dans
 ceci
montre que
ceci
montre que
 .
.
Réciproquement, supposons que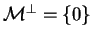 . Si
. Si
 , alors en particulier
, alors en particulier
 .
C'est à dire
.
C'est à dire
 donc
donc  . Ainsi
. Ainsi
 .
Comme
.
Comme
 est un sous-espace fermé de
est un sous-espace fermé de 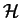 on a
on a
 .
Or
.
Or
 donc
donc
 . Par conséquent
. Par conséquent
 et
et
 .
.

Réciproquement, supposons que