



Next: 6 Annexe
Up: memoire
Previous: 4 Relation entre et
Contents
5 Application à la Théorie Spectrale
Nous avons vu précédemment une première application du théorème de
Hahn-Banach lors de la preuve du théorème
2.2.2, où il est
montré que
On propose maintenant une autre
application, précédée des définitions préliminaires à sa
compréhension.
Je me suis demandé, en rédigeant ce mémoire, s'il était possible de
passer outre le Théorème de Hahn-Banach pour cette application en
rajoutant des hypothèses sur l'espace de Banach

. La première qui
m'est venue à l'esprit fut de prendre

réflexif, mais la
construction de l'isomorphisme canonique entre

et
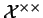
, le biadjoint, nécessite aussi l'utilisation du
théorème de Hahn-Banach. Et finalement, la structure Hilbertienne est
suffisante pour obtenir cela.
La question consistant à savoir, si on peut se passer de Hahn-Banach
pour prouver ce théorème, est-on alors dans un espace de Hilbert, ne
me semble pas dénuée d'intérêt. Peut-être la réponse mènerait-elle à
construire des espaces qui sont ``un peu plus'' que les Banach, et un
``peu moins'' que les Hilberts. Mais la question elle-même est
peut-être mal formulée.
On note

l'ensemble des opérateurs linéaires continus de

dans

où

désignera toujours un espace de Banach.
Sauf précision contraire,
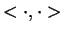
désignera un crochet de
dualité.
L'Ensemble Résolvant. 0.1
L'ensemble résolvant de
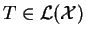
est :
Résolvante de $T$ en $z$. 0.2
Si
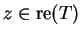
, l'opérateur défini par
, est
appelé résolvante de

en
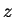
.
Spectre. 0.3
On appelle spectre
8 de

l'ensemble
Ensemble Spectral. 0.4
Soit
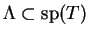
.
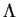
est appelé ensemble spectral de

si
On montre que ceci est équivalent à dire que 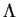 est un
connexe de
est un
connexe de
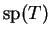 . Pour montrer cela, on démontre que
. Pour montrer cela, on démontre que
 est
un ouvert de
est
un ouvert de
 , ce qui provient directement de la structure
d'algèbre de Banach de
, ce qui provient directement de la structure
d'algèbre de Banach de
 .
.
Définition. 0.5

est une
courbe de Jordan si et seulement si elle est rectifiable, simple et fermée.
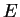
est un
domaine élémentaire de Cauchy si et seulement E est
un ouvert borné connexe de

et que sa frontière est réunion d'un
nombre fini de courbes de Jordan disjointes.
Figure:
La partie hachurée est un domaine élémentaire de Cauchy
|
|
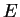
est un
domaine de Cauchy si et seulement si il est réunion
finie de domaines élémentaires de Cauchy dont les adhérences sont
disjointes. La frontière
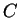
d'un domaine de Cauchy
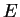
,orientée de
telle sorte que
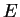
se retrouve à gauche de la courbe s'appelle un
contour de Cauchy. Ainsi dans la figure
3.1
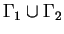
est un
contour de Cauchy. L'ensemble
est appelé l'
intérieur de
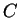
et
l'ensemble
est appelé l'
extérieur de
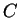
.
Soit
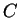
un contour de Cauchy. Si
et

sont des
sous-ensembles de

tels que
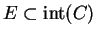
et
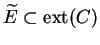
alors on dit que
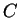 sépare
sépare 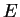
de

.
Théorème. 0.6
Si E est un sous-ensemble compact de

contenu dans un ouvert
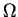
, alors il existe un domaine de Cauchy

tel que
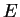
soit
un sous-ensemble de

et l'adhérence de

un sous-ensemble de
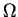
.
Corollaire. 0.7
Soit
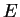
un sous-ensemble compact de

et

un
sous-ensemble fermé de
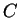
. Si
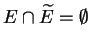
,
alors il existe un contour de Cauchy séparant
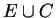
de

, et il existe un contour de Cauchy séparant
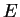
de

Corollaire. 0.8
Soit

un opérateur linéaire borné de

dans

et
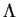
un ensemble spectral de

. Alors d'après le corollaire précédent,
il existe un contour de Cauchy
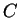
qui
sépare
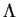
de
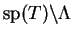
.
Si
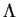
est un ensemble spectral de

, l'ensemble des
contours de Cauchy séparant
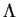
de
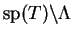
sera noté
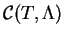
.
Pour un ensemble spectral
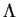
de

et
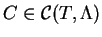
, on définit
Proposition. 0.9
Soit
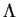
un ensemble spectral de

. Alors
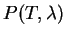
est
un projecteur continu qui commute avec

.
Proof.
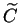
joue le même rôle que
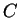
tout en laissant
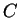
dans
son intérieur, ainsi
or
Donc on réobtient
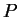
.

commute
avec
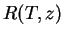
et
est une limite de sommes de Riemann de
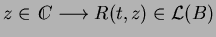
. Comme

est continu,
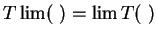
.

Espace Annihilateur. 0.10
Si
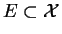
, on appelle espace annihilateur de
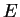
le
sous-ensemble de

suivant :
où

est défini comme en (
2.1).
Lemme. 0.11
Soient

et

deux espaces de Banach complexes et

un opérateur linéaire. Alors
Proof.
[Preuve du lemme]
Soit

alors pour tout
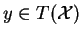
on a
c'est dire
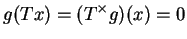
pour tout
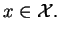
Donc
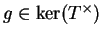
.
Réciproquement, soit
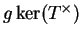
, on a

donc

pour tout
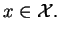
Posant

, on obtient

pour tout
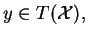
i.e

.

Lemme. 0.12
Soit

un espace de Banach, et
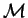
un sous-espace vectoriel de

vérifiant
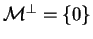
. Alors
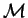
est dense dans

.
Proof.
On procède par contra-posée. Supposons que
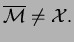 |
(38) |
Comme

est un sous-espace vectoriel, alors d'après
1.1.4 il admet une base
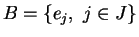
. D'après
(
3.1) cette base n'est pas maximale. Il existe donc

tel que
Soit
Cette application envoie

sur 0 et est de norme

. Elle vérifie
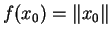
et
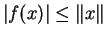
pour tout
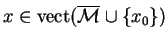
. Alors d'après le théorème
1.2.4 il existe un prolongement

de

à

ayant les mêmes propriétes. Cette application est une
élément du dual envoyant

sur 0. Ainsi
.

Théorème. 0.13
Soit

un espace de Banach complexe et
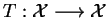
un opérateur
linéaire borné. Alors
-
et
- Soit
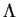 un sous-ensemble de
un sous-ensemble de
 .
.
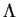 est un ensemble spectral de
est un ensemble spectral de  si et seulement si
si et seulement si
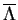 est un ensemble spectral de
est un ensemble spectral de  . On a
alors
. On a
alors
Proof.
a) Soit
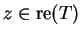
. On a:
On obtient ainsi

car
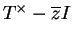
est inversible
et également
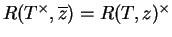
.
Réciproquement, soit
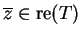
. L'opérateur
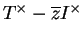
est alors bijectif, donc injectif.
Alors d'après le lemme
3.0.11, on a :
Le
sous-espace
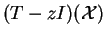
est dense d'après le lemme
3.0.12. Considérons alors

. D'après le théorème
1.2.5 il existe
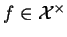
telle que
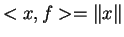
et
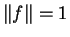
. Alors
L'opérateur

est donc injectif. Comme
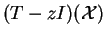
est un
sous-espace vectoriel d'un espace vectoriel complet, il est
complet, donc il est fermé. Comme de plus il est dense, on obtient
Ainsi

est surjectif et donc bijectif. On
a obtenu
b) D'après
a) on sait
Par conséquent, un sous-ensemble
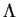
de

est un ensemble
spectral si et seulement si
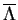
est un ensemble
spectral pour

. Pour toute courbe de Jordan
![$ \Gamma:[a,b]\longrightarrow {\ \rlap{\raise 0.4ex \hbox{$\scriptscriptstyle \vert$}}\hskip -0.2em C}$](img547.png)
, on définit la courbe de Jordan conjuguée
par

pour tout
![$\displaystyle t\in[a,b].$](img549.png)
On a effectué le changement de variable
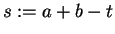
pour
![$ t\in[a,b]$](img557.png)
.
Soit 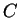 in
in
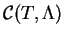 et notons
et notons 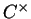 le contour
de Cauchy entourant
le contour
de Cauchy entourant 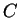 et sa courbe conjuguée. Alors
et sa courbe conjuguée. Alors
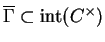 et
et
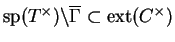 , ainsi
, ainsi
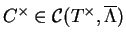 . On obtient alors
. On obtient alors





Next: 6 Annexe
Up: memoire
Previous: 4 Relation entre et
Contents
julien.mary@free.fr
![]() est un
connexe de
est un
connexe de
![]() . Pour montrer cela, on démontre que
. Pour montrer cela, on démontre que
![]() est
un ouvert de
est
un ouvert de
![]() , ce qui provient directement de la structure
d'algèbre de Banach de
, ce qui provient directement de la structure
d'algèbre de Banach de
![]() .
.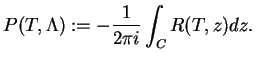

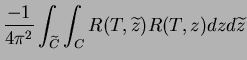
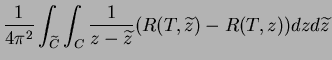
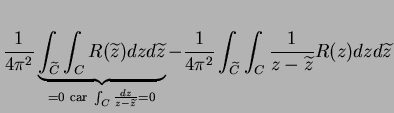
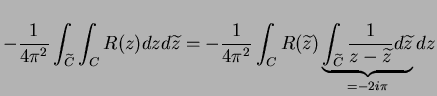
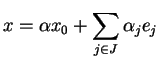
![]()
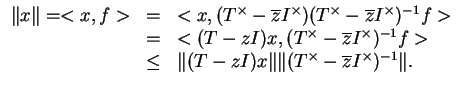
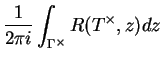
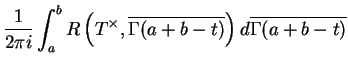
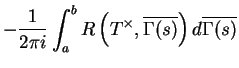
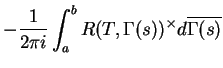
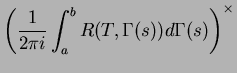
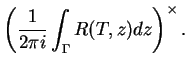
![]() in
in
![]() et notons
et notons ![]() le contour
de Cauchy entourant
le contour
de Cauchy entourant ![]() et sa courbe conjuguée. Alors
et sa courbe conjuguée. Alors
![]() et
et
![]() , ainsi
, ainsi
![]() . On obtient alors
. On obtient alors
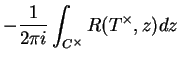
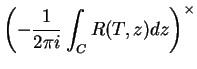
![]()