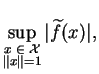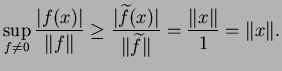Next: 4 Espaces Adjoints
Up: 3 Théorèmes
Previous: 1 Le lemme de
Contents
Le théorème de Hahn-Banach fut proposé
en

par Hans Hahn, puis redécouvert dans sa forme actuelle, plus
générale par Stefan Banach en

et généralisé aux espaces
vectoriels complexes par Bohnenblust et Sobczyk en 1938.
Théorème. 2.1 (Prolongement des fonctionnelles linéaires)
Soit

un

-espace-vectoriel et

une fonctionnelle sous-linéaire sur

.

est un sous-espace-vectoriel de

et

une fonctionnelle
linéaire définie sur

telle que :
Alors il existe

linéaire, prolongeant

à

, vérifiant :
 |
(1) |
Le point essentiel est de montrer que l'on peut prolonger à une
dimension de plus: Si

est linéaire et définie sur

sous-espace-vectoriel de

, de façon à ce que
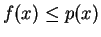
pour
tout

, et si pour

on peut prolonger

en

définie sur

et vérifiant

, alors le reste de la preuve sera constitué de la mise en place
d'une application du lemme de Zorn. On commence donc par le
Lemme. 2.2
Soit

un sous-espace vectoriel du

-espace vectoriel

,
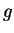
une forme linéaire définie sur

telle que :
Soit

. Alors il existe une forme linéaire

sur

telle que

prolonge
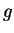
et

sur

.
Proof.
[Démonstration du lemme]
Prolonger
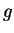
demande seulement de définir
Ce prolongement doit
vérifier :
Si

cette inégalité est verifiée par hypothèse. Si
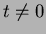
on découpe la propriété en
deux. Soit
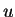
et
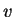
deux réels positifs :
 |
|
|
(2) |
 |
|
|
(3) |
On pose
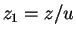
. On obtient alors :
De la même manière en posant

, on obtient :
Ainsi :
Donc :
On a

car l'

porte sur un ensemble non vide de valeurs finies. Idem pour

. Il suffira donc
de prendre pour
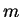
n'importe quel réel de
![$ [S;I]$](img116.png)
. Il reste maintenant à vérifier que :
ce qui équivaut à :
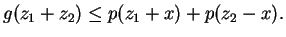 |
(4) |
Or par hypothèse
 . Et comme
. Et comme  est une
fonctionnelle sous-linéaire, on a l'inégalité :
est une
fonctionnelle sous-linéaire, on a l'inégalité :
Donc (
1.4) est vérifiée.

Proof.
[Démonstration du théorème
1.2.1]
Soit

l'ensemble des sous-espaces vectoriels

qui
sont le graphe d'une forme linéaire
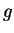
définie sur un sous-espace vectoriel

(variable)
de

contenant

, où la restriction de
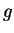
à

est

, et où de plus

On a alors :

contient

(ce qui signifie que
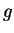
prolonge

), et
Munissons

de la relation d'ordre

d'inclusion des sous-espaces de
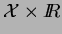
.
L'ordre  est inductif : Si
est inductif : Si
 est une famille totalement
ordonnée de
est une famille totalement
ordonnée de  . Alors
. Alors
est un sous-espace vectoriel. En effet Si

et
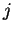
sont dans

avec

, on a

ou bien

car

et

appartiennent à une famille totalement ordonnée de

. Donc

est un sous-espace vectoriel.

est le graphe d'une forme linéaire
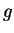
définie sur le sous-espace vectoriel
Cette
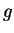
prolonge

et

. Ainsi

. De plus

majore
tous les

. Ainsi l'ordre sur

est inductif.
Application du lemme de Zorn : Soit
 un élément maximal, et
un élément maximal, et
 le sous-espace associé. Montrons que
le sous-espace associé. Montrons que
 . Pour cela supposons
que
. Pour cela supposons
que
 , il existe alors un vecteur
, il existe alors un vecteur
 donc
donc
 et le lemme 1.2.2
donne une extension convenable
et le lemme 1.2.2
donne une extension convenable
 , ce qui contredit la maximalité de
, ce qui contredit la maximalité de  .
Ainsi
.
Ainsi
 ce qui démontre le théorème.
ce qui démontre le théorème.

Tous les énoncés qui suivent sont écris en termes de fonctionnelles linéaires. Néanmoins,
ils restent valables aussi pour des fonctionnelles
antilinéaires
5, lorsque l'espace vectoriel
est sur

.
Théorème. 2.3 (Généralisation au cas complexe)
Soit

un

-espace vectoriel avec

ou

. L'application
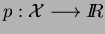
est sous-linéaire.

est un sous-espace-vectoriel de

et

une fonctionnelle
linéaire définie sur

telle que :
 |
(5) |
Alors il existe

linéaire, prolongeant

à

, vérifiant :
 |
(6) |
Proof.
Si

, on a
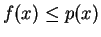
pour tout

d'après (
1.5). D'après le théorème
1.2.1
il existe un prolongement à

de

que l'on note

, vérifiant
 |
(7) |
Combinant (
1.7) et le fait que

soit positivement homogène,
on obtient
ce qui donne (
1.6).
Si
 ,
,
 est aussi un espace vectoriel complexe et on va commencer
par les considérer tous deux comme des espaces vectoriels réels en parlant des parties réelles et imaginaires
des fonctionnelles considérées et en se restreignant à des scalaires réels. On note
est aussi un espace vectoriel complexe et on va commencer
par les considérer tous deux comme des espaces vectoriels réels en parlant des parties réelles et imaginaires
des fonctionnelles considérées et en se restreignant à des scalaires réels. On note
 et
et
 les espaces
les espaces
 et
et
 vus ainsi. On écrit donc
vus ainsi. On écrit donc
où

et

sont à valeurs réelles. La linéarité de

sur

donne immédiatement celles de

et

sur

.
Il est clair que

et donc avec (
1.5) on obtient

pour tout

.
Il existe donc d'après le théorème
1.2.1 un prolongement linéaire

de

à
.
vérifiant
 pour tout pour tout 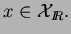 |
(8) |
Le même raisonnement donne un prolongement
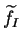
de

à
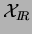
.
Retournons sur

où l'on a

. Alors pour tout

, on a
Les parties réelles devant être égales entre elles, on obtient
 pour tout pour tout  |
(9) |
Par conséquent, on pose pour tout

 |
(10) |
D'après la relation (
1.9), il est clair que

.
Le prolongement défini par (1.10) est linéaire.
Soit
 un complexe de partie réelle
un complexe de partie réelle  et de partie imaginaire
et de partie imaginaire  . Alors
. Alors
 vérifie (1.6).
vérifie (1.6).
Si  est tel que
est tel que
 alors (1.6) est vérifiée car
alors (1.6) est vérifiée car  est une semi-norme 6.
Soit
est une semi-norme 6.
Soit  tel que
tel que
 , alors
, alors
Donc
Comme

est réel on obtient en utlisant (
1.10) et le fait que

est positivement homogène,

Théorème. 2.4 (Le prolongement conserve la norme)

est un sous-espace vectoriel du

-espace vectoriel

et

une fonctionnelle linéaire définie sur

.
Alors il existe

prolongeant

à

et
de même norme. Ces normes étant définie par :
Proof.
Si

alors

est nulle, on la prolonge par l'application nulle.
Si

alors pour tout

on a
Et la fonctionnelle

du théorème
1.2.3 est définie par
Donc il existe

définie sur

vérifiant pour tout

En prenant le
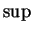
pour tout

de norme

, on obtient
D'autre part, puisque
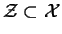
, l'inégalité

est aussi
vérifiée.

Le théorème qui suit possède un corollaire intéressant permettant de séparer les point de l'espace

, ce
qui signifie que si

et

sont différents, il existe une fonctionnelle linéaire

envoyant

et

sur des points
différents.
Théorème. 2.5 (Fonctionnelles linéaires bornées)

est un espace vectoriel normé et

. Alors il existe une fonctionnelle
linéaire

définie sur

telle que :

et

Proof.
Cette application est de norme

et d'après le théorème
1.2.4, il existe une fonctionnelle linéaire

prolongeant

à

, de même norme. De plus

.

Corollaire. 2.6
Soit

un espace vectoriel normé. Alors :
De plus, si

pour toute fonctionnelle linéaire

, définie sur

, alors

.
Proof.
Soit

, alors d'après le théorème précédent
Et de l'inégalité

, on a





Next: 4 Espaces Adjoints
Up: 3 Théorèmes
Previous: 1 Le lemme de
Contents
julien.mary@free.fr



![]() . Et comme
. Et comme ![]() est une
fonctionnelle sous-linéaire, on a l'inégalité :
est une
fonctionnelle sous-linéaire, on a l'inégalité :
![]() est inductif : Si
est inductif : Si
![]() est une famille totalement
ordonnée de
est une famille totalement
ordonnée de ![]() . Alors
. Alors

![]() un élément maximal, et
un élément maximal, et
![]() le sous-espace associé. Montrons que
le sous-espace associé. Montrons que
![]() . Pour cela supposons
que
. Pour cela supposons
que
![]() , il existe alors un vecteur
, il existe alors un vecteur
![]() donc
donc
![]() et le lemme 1.2.2
donne une extension convenable
et le lemme 1.2.2
donne une extension convenable
![]() , ce qui contredit la maximalité de
, ce qui contredit la maximalité de ![]() .
Ainsi
.
Ainsi
![]() ce qui démontre le théorème.
ce qui démontre le théorème.
![]()
![]() ,
,
![]() est aussi un espace vectoriel complexe et on va commencer
par les considérer tous deux comme des espaces vectoriels réels en parlant des parties réelles et imaginaires
des fonctionnelles considérées et en se restreignant à des scalaires réels. On note
est aussi un espace vectoriel complexe et on va commencer
par les considérer tous deux comme des espaces vectoriels réels en parlant des parties réelles et imaginaires
des fonctionnelles considérées et en se restreignant à des scalaires réels. On note
![]() et
et
![]() les espaces
les espaces
![]() et
et
![]() vus ainsi. On écrit donc
vus ainsi. On écrit donc
![]() un complexe de partie réelle
un complexe de partie réelle ![]() et de partie imaginaire
et de partie imaginaire ![]() . Alors
. Alors
![]() vérifie (1.6).
vérifie (1.6).
![]() est tel que
est tel que
![]() alors (1.6) est vérifiée car
alors (1.6) est vérifiée car ![]() est une semi-norme 6.
Soit
est une semi-norme 6.
Soit ![]() tel que
tel que
![]() , alors
, alors