A un opérateur linéaire continu
 défini sur l'espace vectoriel normé
défini sur l'espace vectoriel normé
 on peut associer un autre opérateur linéaire ,
appelé opérateur adjoint de
on peut associer un autre opérateur linéaire ,
appelé opérateur adjoint de  . On le note
. On le note
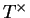 .
L'intérêt pour cet opérateur est motivé par son utilité dans la résolution d'équations
faisant intervenir des opérateurs. Citons les équations intégrales linéaires faisant intervenir
des opérateurs compacts. De telles équations apparaissent de manière naturelle
en physique. Dans cette section on définit l'opérateur adjoint,on démontre certaines de ses
propriétés et on fait le lien avec l'opérateur adjoint
.
L'intérêt pour cet opérateur est motivé par son utilité dans la résolution d'équations
faisant intervenir des opérateurs. Citons les équations intégrales linéaires faisant intervenir
des opérateurs compacts. De telles équations apparaissent de manière naturelle
en physique. Dans cette section on définit l'opérateur adjoint,on démontre certaines de ses
propriétés et on fait le lien avec l'opérateur adjoint  dans le cas hilbertien. Il est important de préciser que cette discussion va dépendre
du théorème 1.2.5 sans lequel rien ne serait ici possible.
dans le cas hilbertien. Il est important de préciser que cette discussion va dépendre
du théorème 1.2.5 sans lequel rien ne serait ici possible.
![$\displaystyle \xymatrix @H=0pt{ \mathcal{X}\ar[rr]^T \ar[dr]_f & & \mathcal{Y}\ar[dl]^g \\ & {I\!\!K}& }$](img287.png)

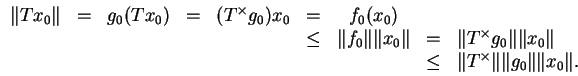
![$\displaystyle \xymatrix @H=0pt{ \mathcal{X}\ar[r]_T \ar@/^1pc/[rr]^{ST} & \mathcal{Y}\ar[r]_S & \mathcal{Z}\\ }$](img324.png)
![$\displaystyle \xymatrix @H=0pt{ \mathcal{X}^* & \ar[l]_{T^\times} \mathcal{Y}^* &\ar[l]_{S^\times} \ar@/^1pc/[ll]^{T^\times S^\times} \mathcal{Z}^* }$](img325.png)