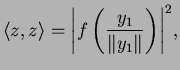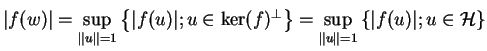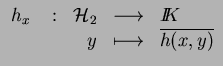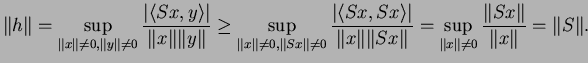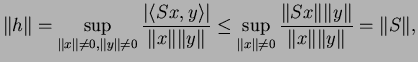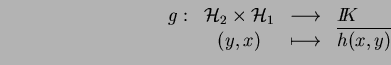Théorème d'isomorphie de Riesz. 3.1
Soit
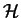
un espace de Hilbert. Toute fonctionnelle linéaire (respectivement antilinéaire) continue
sur
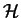
peut être écrite en termes de produit scalaire, c'est à dire
où
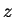
dépendant de

est déterminé de manière unique. De plus
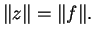 |
(29) |
Autrement dit, les espaces
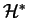
et
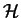
sont isomorphes et isométriques.
L'application
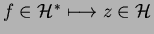
est antilinéaire (respectivement linéaire).
Proof.
Soit

fixé et considérons l'application linéaire
Le théorème
2.3.1 nous fournit un élément unique
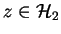
tel que pour tout
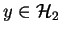
on a
c'est à dire
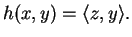 |
(31) |
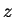
étant unique et dépendant de

, cela définit un opérateur
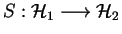
tel que

.
Une substitution dans (
2.20) nous donne (
2.19).
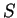 est linéaire :
est linéaire :
Soient
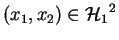
,
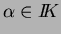
et
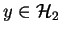
. Alors
Comme cela est vrai pour tout

, on a
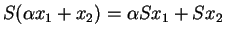
.
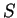 est continue :
est continue :
On a
De plus
donc
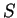 est unique :
est unique :
Supposons qu'il existe
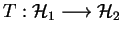
tel que pour tout
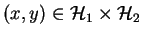
on ait
Fixons

. Alors
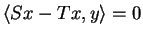
pour tout

, donc
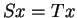
. Comme ceci est vrai pour tout

, on
obtient
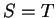
.

![]() dans
dans
![]() et posons
et posons
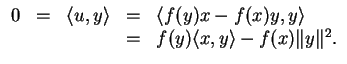
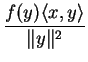
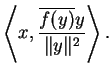
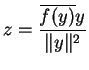 convient.
convient.
![]() .
Et on obtient à nouveau
.
Et on obtient à nouveau ![]() , défini par la même expression.
, défini par la même expression.
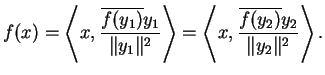
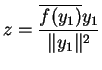 et donc
et donc