Stefan Banach est né le 30 mars 1892 à Kraków en Autriche-Hongrie. Son
père s'appelait Stefan Greczek et sa mère Katarzyna Banach.
Elle s'évanouit dans la nature quatre jours après sa naissance sans laisser de traces.
On ne connaît rien de plus à son propos. Plus tard Banach la rechercha mais son père refusa de lui dire quoi que ce soit, mis à part le fait qu'il avait juré de ne rien dévoiler de sa véritable identité. Certains pensent qu'elle était en fait la servante de sa mère, d'autres, sa nourrice. Stefan Greczek est né dans un petit village nommé Ostrowsko, à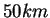 au sud de Kraków. C'est ici, dans la maison de sa
grand-mère que Banach fut amené après son baptême. Lorsque celle-ci
tomba malade, Stefan Greczek fit en sorte que Banach soit recueilli
par Franciszka Plowa, laquelle habitait Kraków avec sa soeur Maria. Le
tuteur de Maria était un intellectuel français du nom de Julius Mien,
et il reconnut très tôt les talents que Banach possédait. Mien lui
apprit le français et lui donna en général le goût pour les études.
au sud de Kraków. C'est ici, dans la maison de sa
grand-mère que Banach fut amené après son baptême. Lorsque celle-ci
tomba malade, Stefan Greczek fit en sorte que Banach soit recueilli
par Franciszka Plowa, laquelle habitait Kraków avec sa soeur Maria. Le
tuteur de Maria était un intellectuel français du nom de Julius Mien,
et il reconnut très tôt les talents que Banach possédait. Mien lui
apprit le français et lui donna en général le goût pour les études.
On ne connaît rien de plus à son propos. Plus tard Banach la rechercha mais son père refusa de lui dire quoi que ce soit, mis à part le fait qu'il avait juré de ne rien dévoiler de sa véritable identité. Certains pensent qu'elle était en fait la servante de sa mère, d'autres, sa nourrice. Stefan Greczek est né dans un petit village nommé Ostrowsko, à